适用于任意level DAC的树形DEM

论文名称

Tree-Structured DEM DACs with Arbitrary Numbers of Levels

Rakuljic, Nevena, and Ian Galton. “Tree-structured DEM DACs with arbitrary numbers of levels.” IEEE Transactions on Circuits and Systems I: Regular Papers 57.2 (2009): 313-322.

论文摘要

等权重树形DEM DAC被广泛应用在DSM中来保证理论上完全相同的模拟器件之间的失配只会带来shaped noise的上升，而不是非线性失真。树形DEM相比其他DEM有优势，但是缺点在于只适用于2^N个element的DAC。当应用到非2^N个element DAC的DSM中时，需要的DEM控制的元素会超出实际能用到的DAC element，这会导致功耗和面积的浪费。因此本文提出了一种能够应用于任意level DAC的等权重树形DEM。

论文内容

DAC输出的构成

DAC的输出由三部分组成，signal pulse sequence、offset pulse sequence以及DAC Noise，分别对应下式中的$\alpha$、$\beta$和edac。针对DAC的整形即是针对edac的整形。

给出$\alpha$和$\beta$的公式如下所示。

其中的$\alpha_i$和$\beta_i$如下所示。

而其中的ehi与eli分别代表输出为高与低时的mismatch error pulse，即包含mismatch error的输出脉冲。其中的a(t)为unit output pulse，且在0 <= t < T外均为0，delta则为x[n]的最小步进。

DAC(u,w)的定义

对于任意满足1<=u<=w<=N的u与w的值，DAC(u,w)是一组包含了编码器与跟随的1-bit DAC单元的模块。针对输入信号有如下定义。

按照(u,w)这个操作的定义可知，输出的定义为如下。

其中y_i(t)代表第i个1-bit单元在第n个周期时的采样输出：

将y(t)代入y(u,w)(t)推广可得如下公式：

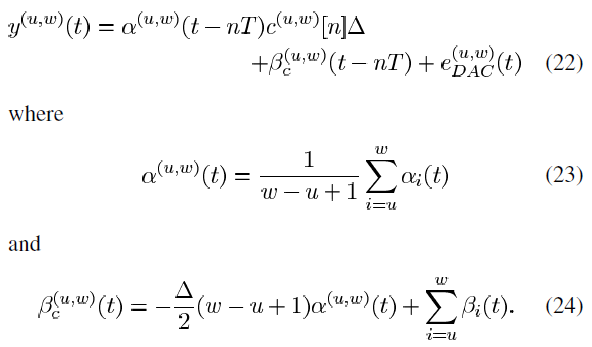
特别地，当u=w时得到单比特DAC的本征线性，对比(6)与(22)，如下：

针对DAC控制电路与DAC单元的等价

DAC模块存在一个编码器Encoder与DAC阵列，将DAC分为(1,g,N)时，可以将其等价为由一个Switching Block和两个sub DAC组成。

推广(1,g,N)到(u,v,w)可得如下图所示。

其中的S(u,v,w)被称为switching sequence，它在控制DAC Noise中扮演了一个关键的角色。将S(1,g,N)的表达式可以推广到任意的1<=u<=v<=w<=N，如下图所示。

因此可以给出一个较为实际的可以实现的DAC的控制逻辑，如下所示。

其中的G^(u,v,w)和s^(u,v,w)[n]如下所示。

01.对于N bit的DAC的tree-structure encoder，存在N-1个switching block，可用递归方
法推导

02.不止一种等价的tree-structure 编码方式

DEM encoder的实现

s^(1,g,N)[n]的实现可以分为两种情况。首先给出在树形结构下DAC输出一定满足的两个公式：

极端情况：当输入为0或者N的时候

此时，为了满足公式(40)和公式(41)，那么对于输入0必定存在c^(1,g)[n]=c^(g+1,N)[n]=0，对于输入N必定存在c^(1,g)[n]=g且c^(g+1,N)[n]=N-g。所以代入公式(35)可得switching sequence即s^(1,g,N)[n]为0。

其他的输入

此时至少存在两种选择方式，由公式(35)可知，如下所示，其中<b>表示b减去floor(b)，即b的分数部分，如下图所示。

将公式(42)减去公式(34)可得如下DAC输出两部分的值所示：

因此扩展得到s^(u,v,w)[n]值如下所示(这只是其中一种Encoder的设计思路，但是已经足够能够得到噪声性能了)：

1. 当Tree-Structure Encoer满足公式(45)的时候，那么从Encoder出来的N个1-bit输出序列将满足公式(17)，并且DAC的噪声将满足公式(39)，公式(39)也说明，DAC的噪声的统计学属性由switching sequences决定。

2. DEM DAC不引入非线性的一个必要条件就是，针对所有的t，edac(t)均为0，此结果与mismatch error pulse和x[n]均无关。所以由公式(45)可以看出，其存在符号相反的正负两种选择，因此存在让edac(t)=0 for all t 的情况。

DEM设计实例

考虑一个12Elements的DAC，那么s(1,4,12)[n]需要满足公式(48)，这是从公式(45)推导出来的。

那么为了保证DAC的输出与输入序列c[n]无关，也就是说s(1,4,12)[n]的数学期望为0，那么便存在公式(49)。

考虑c[n]为{2,5,8,11}的例子，只有当{s(1,4,12)[3k],s(1,4,12)[3k+1],s(1,4,12)[3k+2]}在{1/3,1/3,-2/3}、{1/3,-2/3,1/3}与{-2/3,1/3,1/3}中按照均匀分布选择时，才能既满足数学期望为0，又满足与输入序列无关，因此这个序列就被highpass shaped，并且杂散音也被消除了。

其针对2-5-8-11的RTL级实现电路实现可以采用LFSR实现，如下图所示。

同理，{1,4,7,10}由于其概率与{2,5,8,11}一致，所以可以通过取反的方式实现，如下图所示可以将两者整合到一起。

针对剩下的每一个(u,v,w) !== (1,4,12)进行s(u,v,w)的设计，其中λ在±1/2中均匀选取，如下图所示。

给出针对奇偶分类的RTL级实现如下所示。

给出Tree-Structure的两种实现结构如下图所示，这两种结构的实现方式都是等价的。

Tree-Structure中Delay产生的原因

delay主要来源于s^(u,v,w)[n]模块。

• 有多少级switching block
• 每一级switching block 转换有多快