适用于多比特DSM的低复杂度高阶VMS

论文名称

Low-Complexity High-Order Vector-Based Mismatch Shaping in Multibit ΔΣ ADCs

Sun, Nan, and Peiyan Cao. “Low-Complexity High-Order Vector-Based Mismatch Shaping in Multibit $\Delta\Sigma $ ADCs.” IEEE Transactions on Circuits and Systems II: Express Briefs 58.12 (2011): 872-876.

论文摘要

本论文提出的VMS设计拥有低复杂度，它的复杂度只随DAC的elements个数线性增长。而与已有的低复杂度VMS比较，它又不需要额外的Filter，并且它还拥有更好的mismatch整形效果和更好的稳定性。

论文内容

论文分为两部分，第一部分给出了前置的参考论文，第二部分在此基础上进行了改进，得到了本文的结构。

前置论文

A. Yasuda, H. Tanimoto, and T. Iida, “A third-order Δ−Σ modulator using second-order noise-shaping dynamic element matching,” IEEE J. Solid-State Circuits, vol. 33, no. 12, pp. 1879–1886, Dec. 1998.

传统的VMS存在一个缺点，那就是很高的硬件复杂度。其中的排序模块Sorter，因为要针对N个变量进行高速的完全排序，此时复杂度呈N²增长。为了减小复杂度，可以采用部分排序，可以将复杂度的增长变为N。如下图所示。

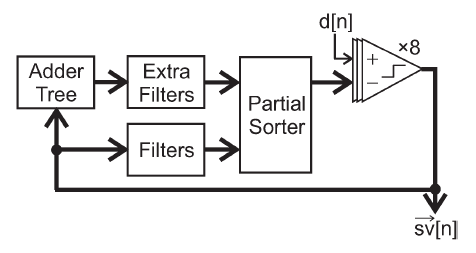
缺点：

• 需要N-1个额外的filters，这些filters占据了芯片空间并且消耗了额外的power
• mismatch整形效果和稳定性都变差了，相比Std VMS来说，对N=8的情况噪底抬升20dB，对于N>=16的情况此技术不稳定
• 此技术只准确比较了相邻两个element的大小，导致了很大的vector quantization noise

本论文

此论文基于前置论文的结构，修改了结构来去掉了额外的filters，并且通过设计新的partial sorter和新的filter来提高了整形效果和稳定性

新的原理图

由于滤波是个线性操作：先加再滤波等效于先滤波再加，所以在此原理上修改了前置论文的结构图。通过此方法消除了额外的filters的使用，这几乎在不消耗任何代价的情况下就将前置论文的面积减小了50%。

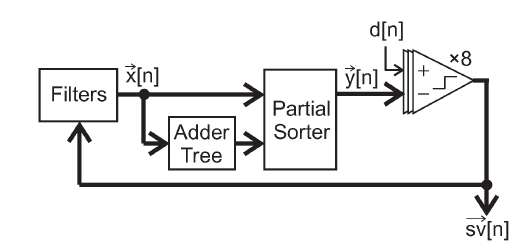
新的滤波器

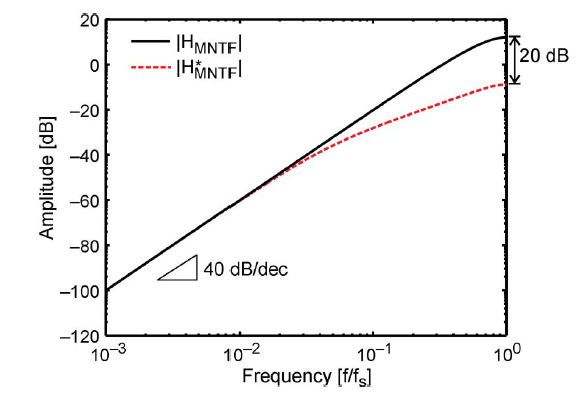
提高整形效果与稳定性的关键在于设计一个新的filter，由于标准的二阶整形滤波器的MTF是(1-Z^-1)²，因此它的频响如下图所示，它的高频增益是远远大于1的。对于Std VMS来说，高的带外增益是可行的，因为Std VMS的完全排序所产生的vector quantization noise很小，但是对于前置论文提出的相邻element的部分排序就不可行了，因为不完全排序所带来的vector quantization noise非常大。

下图(a)得到的传输函数是(1-Z^-1)²，为了在保证低频的整形效果不受影响的情况下，降低高频的增益，便需要将前馈通路的增益从2变为8，即图(b)。

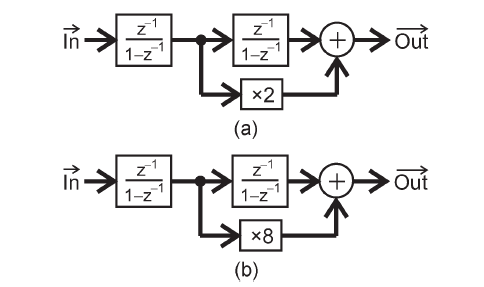
推导其TF可得如下公式：

$F^{*}(z)=8*\frac{z^{-1}}{1-z^{-1}}+(\frac{z^{-1}}{1-z^{-1}})^{2}=\frac{(8-7z^{-1})z^{-1}}{(1-z^{-1})^{2}} (3)$

进而得到的MNTF可得如下公式：

$H^{*}_{MNTF}(z)=\frac{1}{1+F^{*}(z)}=\frac{(1-z^{-1})^{2}}{1+6z^{-1}-6z^{-2}} (4)$

即其在高频的增益比(1-Z^-1)²更低，提高了稳定性，如下图所示。当然这里有一个更直观的理解：前馈增益代表了一阶与二阶的相对关系，当前馈增益大的时候，一阶占比高，这就是说输出更接近一阶，当前馈增益无穷大的时候，输出就是一个一阶，此时是无条件稳定。

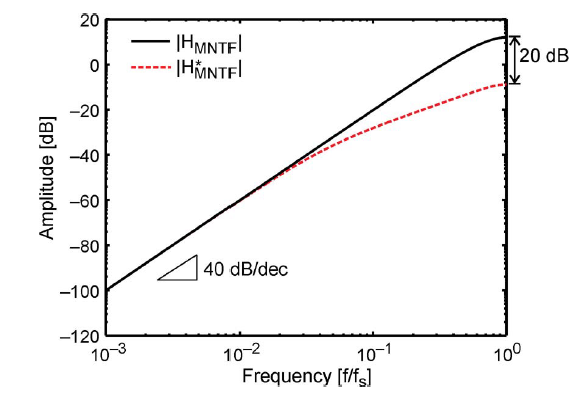
需要注意的是：前馈增益8可以变得更高来进一步提高稳定性，但是因为本身就已经稳定了，所以没有必要这么做。而且选择8的原因也在于，可以简单地将2的位数移动3bit。

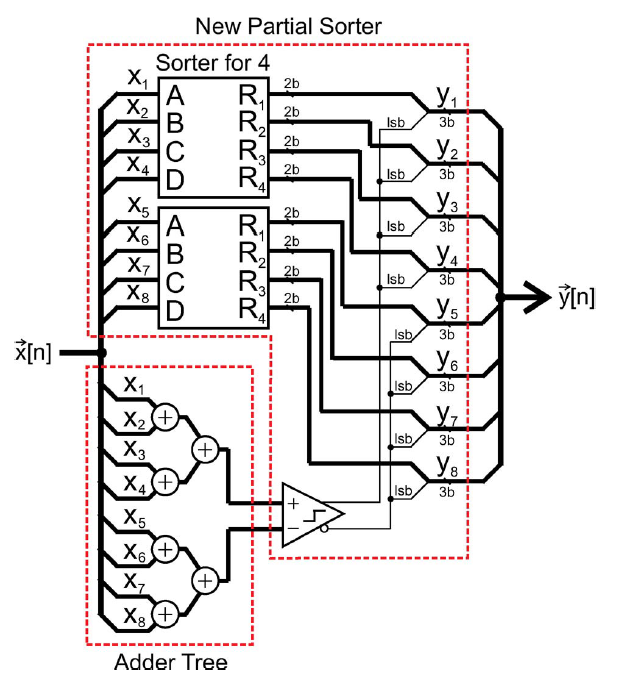
新的部分排序

新的部分排序采用了切2片的方法，在8个element中将其分为4/4两个完全排序，降低了复杂度。如下图所示。需要注意的是，这种实现只适用于2^N个element的DAC。想要实现非2^N的部分排序，参考采用了低成本2阶VQDEM的0.37mm2 250KHz-BW 95dB-SNDR的CTDSM

总结

给出前置论文与本论文提出的以及Std VMS的性能对比。

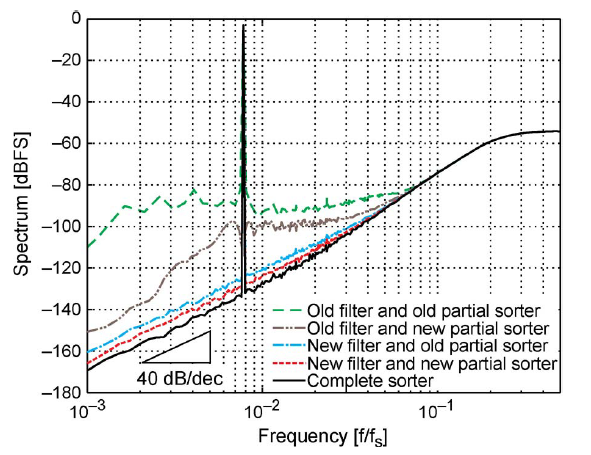
同时给出SNR与复杂度的对比。

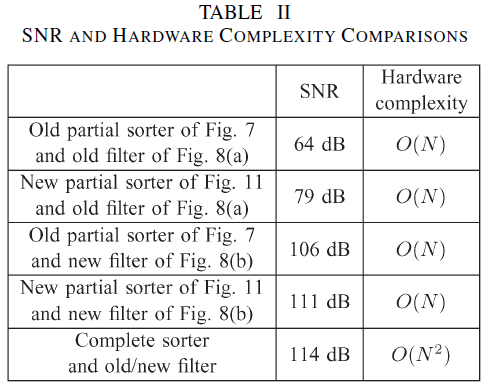
可见，PSVMS在复杂度上与N的增加呈线性相关，在性能上十分接近StdVMS。